Бесконечная сила. Как математический анализ раскрывает тайны вселенной - читать онлайн книгу. Автор: Стивен Строгац cтр.№ 34

Сегодня мы используем координатную плоскость для построения графиков зависимости между переменными. Например, рассмотрим зависимость количества калорий от моих порой позорных привычек в еде. Иногда я позволяю себе пару кусочков хлеба с корицей и изюмом на завтрак. На упаковке написано, что каждый ломтик содержит колоссальные 200 калорий ^[154]. (Если бы я хотел есть более здоровую пищу, то мог бы довольствоваться зерновым хлебом, который покупает жена, в нем всего 130 калорий, но в нашем примере я предпочитаю хлеб с корицей и изюмом, потому что 200 – более удобное число с математической точки зрения, пусть и худшее в смысле калорийности, чем 130.)

Вот график числа калорий, которые я получаю вместе с одним, двумя или тремя ломтиками хлеба.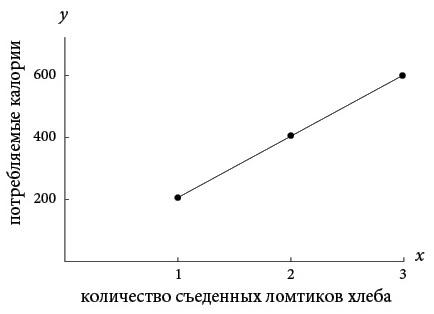

Поскольку в каждом кусочке 200 калорий, то в двух кусках их будет 400, а в трех – 600. Если нанести эти три точки на график, все они окажутся на прямой линии, то есть у нас получается линейная зависимость между числом съеденных кусков и количеством калорий. Если мы обозначим буквой x число кусков, а буквой y – число употребленных калорий, то линейную зависимость можно записать в виде y = 200x. Эту формулу можно использовать для любого количества хлеба. Например, полтора ломтика дадут 300 калорий, и соответствующая точка будет лежать на той же построенной прямой. Поэтому имеет смысл соединять все точки на таких графиках.

Я понимаю, что все это может показаться очевидным, но тем не менее хотел подчеркнуть, что в прошлом это было очевидно не всегда – ведь кто-то же должен был придумать изображать зависимость на такой абстрактной диаграмме. Это не всегда очевидно и сегодня, по крайней мере для детей при их первом знакомстве с подобными графиками.

Здесь есть определенный творческий подход. Прежде всего представление употребления пищи в виде картинки. Это требует гибкости ума. В калориях нет ничего графического. На графике нет реалистичного изображения изюминок и завитков корицы, вложенных в хлеб. Наш график – абстракция, но он дает возможность взаимодействовать различным областям математики: области чисел, таких как число калорий и ломтиков хлеба, области отношений вроде y = 200x и области форм, где есть две перпендикулярные оси, а точки лежат на прямой линии. Благодаря этому слиянию идей скромная диаграмма сочетает числа, зависимости и формы, позволяя объединять арифметику, алгебру и геометрию. Различные ветви математики столетиями работали по отдельности, а теперь слились воедино. (Вспомните, что древние греки ставили геометрию выше арифметики и алгебры и не позволяли им смешиваться, по крайней мере не часто.)

Еще одно слияние относится к горизонтальной и вертикальной осям. Их часто называют осью x и осью y – по переменным, которыми мы их обычно обозначаем. Эти оси – числовые прямые. Подумайте об этом термине: числовые прямые. Числа представлены в виде точек на какой-то прямой. Арифметика соединена с геометрией, причем еще до того, как мы наносим какие-то данные!

Древние греки просто бы истошно орали при таком нарушении протокола. Для них числа означали исключительно дискретные количества, например целые числа и дроби. Напротив, непрерывные количества, такие как длина какой-нибудь линии, считались величинами – принципиально другими сущностями, отличными от чисел. Таким образом, почти два тысячелетия от Архимеда до начала XVII века числа не рассматривались как эквивалент континуума точек на прямой. В этом смысле идея числовой прямой была радикальным нарушением. Сегодня мы даже не задумываемся об этом и ждем, что ученики начальной школы поймут, что числа могут быть наглядно представлены таким образом.

С точки зрения древних греков здесь имеется еще одно богохульство – график полностью пренебрегает сравнением подобного с подобным, скажем яблок с яблоками или калорий с калориями. Вместо этого он показывает ломтики хлеба на одной оси и калории на другой. Их нельзя сравнивать напрямую, и тем не менее мы, не моргнув глазом, делаем это с помощью графиков. Мы просто преобразуем калории и ломтики в числа, означающие действительные числа, бесконечные десятичные дроби, универсальную валюту современной математики. Греки проводили четкие различия между длинами, площадями и объемами, но для нас это просто действительные числа.

Уравнения как кривые

Безусловно, Ферма и Декарт никогда не использовали координатную плоскость для изучения таких осязаемых вещей, как хлеб с корицей и изюмом. Для них она была инструментом изучения чистой геометрии.

Работая независимо друг от друга, каждый из них заметил, что любое линейное уравнение (то есть уравнение, где переменные x и y появляются только в первой степени) дает прямую линию на координатной плоскости. Такая связь между линейными уравнениями и прямыми предполагала возможную связь между нелинейными уравнениями и кривыми. В линейное уравнение вроде y = 200x переменные x и y входят в первой степени, а не возводятся во вторую, третью и любую более высокую степень. Ферма и Декарт поняли, что в ту же игру можно играть с другими степенями и уравнениями. Они могли бы составить любое уравнение, какое пожелают, сделать с x и y все что угодно – возвести одну переменную в квадрат, а другую в куб, перемножить их, сложить, да все что заблагорассудится, – а затем интерпретировать результат как кривую. С определенным везением она может оказаться интересной, возможно, даже такой, которую никто никогда не представлял, а Архимед никогда не изучал. Любое уравнение с x и y становилось новым приключением. Одновременно изменялась точка зрения: вместо того чтобы смотреть на кривую, вы начинали с уравнения и смотрели, какого рода кривую оно дает. Пересадите геометрию на заднее сиденье и дайте управлять алгебре.

Ферма и Декарт начали с рассмотрения квадратных уравнений. В них, кроме констант (например, 200) или линейных членов x и x², должны быть переменные во второй степени, то есть квадратичные члены, такие как y, xy или y². Возведение в квадрат традиционно интерпретировалось как поиск площади, то есть x² означало площадь квадрата со стороной x. В древности площадь считалась величиной, принципиально отличной от длины или объема. Однако для Ферма и Декарта x² было всего лишь еще одним действительным числом; это означало, что его можно отобразить на числовой прямой – ровно так же, как x, x³ или любую иную степень x.

Сегодня предполагается, что даже школьники умеют строить графики уравнений наподобие y = x², и соответствующая кривая оказывается параболой. Примечательно, что все уравнения, содержащие квадратичные члены по x и y, но не включающие члены более высоких степеней, дают кривые только четырех возможных типов: параболы, эллипсы, гиперболы и окружности. Это все. (Если не считать некоторых вырожденных случаев, когда появляются прямые, точки или графика нет вообще, но эти редкие странности мы можем смело игнорировать.) Например, квадратное уравнение xy = 1 дает гиперболу, x² + y² = 4 – окружность, а x² + 2y² = 4 – эллипс. Даже такая страшная на вид зависимость, как x² + 2xy + 2y² + x + 3y = 2 должна быть одним из четырех вышеуказанных вариантов. Оказывается, это парабола.